Design Software History: Evolution of Spline Modeling: From Bézier Curves to NURBS in Design Software History

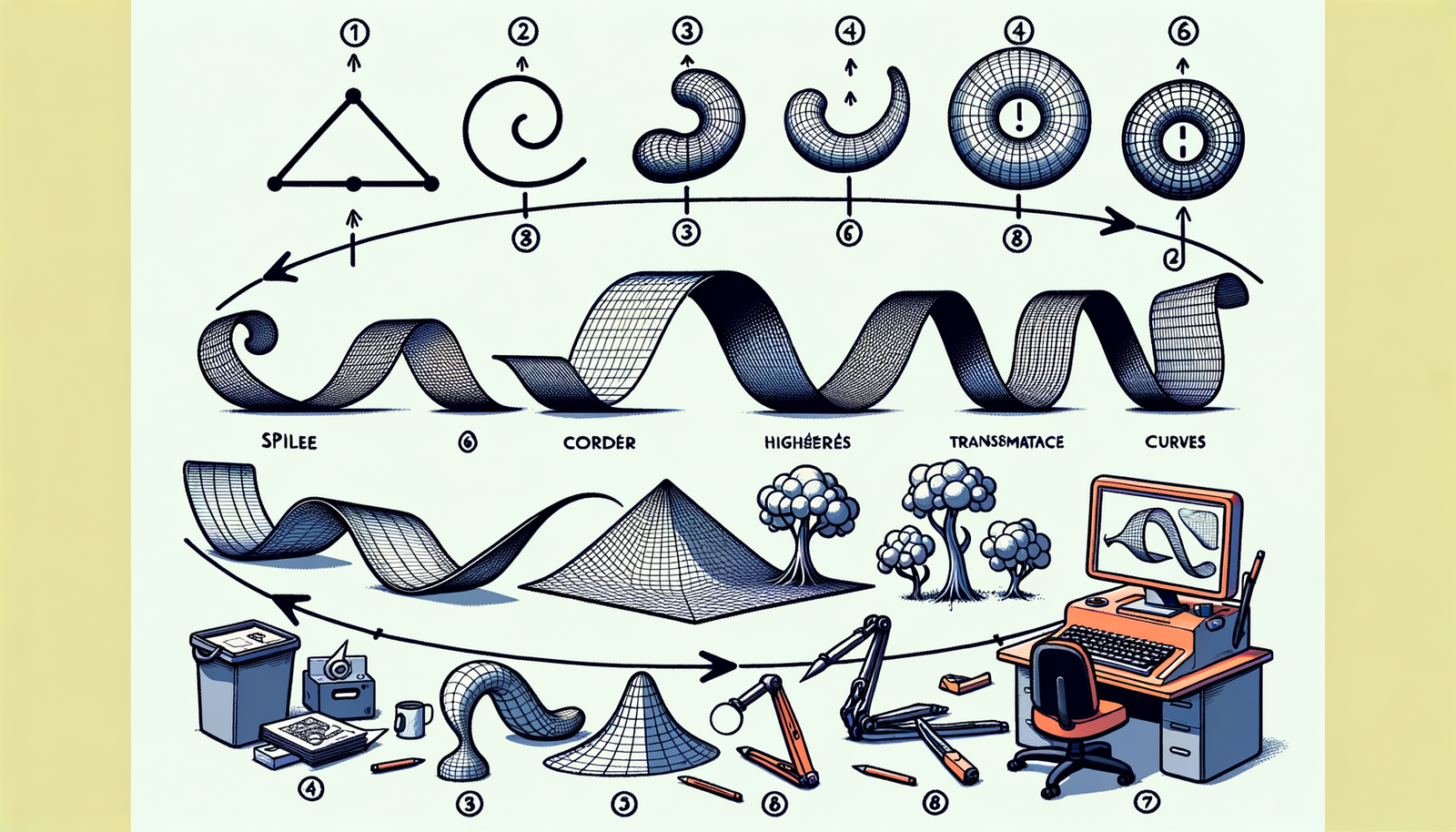
Design software has undergone extensive transformation over the past few decades, significantly influencing various industries. One of the most groundbreaking advancements in the realm of design software is spline modeling, a technique that has revolutionized the way complex shapes are created and manipulated. This article delves into the captivating history of spline modeling, exploring its origins, advancements, and profound impact on multiple industries.

Introduction to Spline Modeling

Definition and Importance

Spline modeling is a mathematical technique used to create smooth and flexible curves and surfaces in computer graphics. It is integral to the creation of complex shapes that are difficult to achieve using traditional geometric modeling techniques. Spline modeling has become a cornerstone in fields such as automotive design, aerospace engineering, and animation, allowing for the precise and efficient creation of intricate designs.

Historical Context

The evolution of spline modeling can be traced back to the nascent days of computer graphics when the need for more flexible and accurate modeling techniques became apparent. Early geometric modeling techniques, while useful, were limited in their ability to create smooth and continuous curves. These limitations spurred the development of splines, which offered a more versatile approach to modeling complex shapes.

Early Developments and Pioneers

Pioneering Work by Pierre Bézier and Paul de Casteljau

The development of spline modeling owes much to the pioneering work of Pierre Bézier and Paul de Casteljau. Pierre Bézier, a French engineer working at Renault, developed the Bézier curve in the 1960s. His work was motivated by the need to create smooth curves for designing car bodies. Bézier's curves quickly gained recognition for their ability to model complex shapes with high precision.

Concurrently, Paul de Casteljau, working at Citroën, developed the De Casteljau algorithm. This algorithm provided a computationally efficient method for calculating points on a Bézier curve, further enhancing the practical utility of spline modeling. Together, Bézier and de Casteljau's contributions laid the foundation for modern spline modeling techniques.

Mathematical Foundations

The mathematical principles underpinning Bézier curves and B-splines are rooted in the concept of control points. Control points are a set of predefined points that influence the shape of the spline. In a Bézier curve, the curve is defined by a series of control points, with the position of each point affecting the curve's overall shape. The mathematical formulation of Bézier curves involves polynomial equations that interpolate the control points, resulting in a smooth and continuous curve.

B-splines, or Basis splines, are a generalization of Bézier curves and offer greater flexibility in curve modeling. B-splines are defined by a sequence of control points and a set of basis functions that determine the influence of each control point on the curve. The use of basis functions allows for the creation of complex and intricate shapes, making B-splines a powerful tool in geometric modeling.

Advancements in Spline Technology

Refinement and Optimization

One of the significant advancements in spline modeling was the development of Non-Uniform Rational B-Splines (NURBS). NURBS extended the capabilities of traditional B-splines by incorporating weights and non-uniform parameterization. This allowed for greater control over the shape of the curve and enabled the modeling of more complex geometries. NURBS quickly became the standard in many industries due to their versatility and precision.

Key contributions to the development of NURBS came from researchers such as Carl de Boor and institutions like the Boeing Company. Their work in refining and optimizing spline technology paved the way for its widespread adoption in various applications, from aircraft design to computer graphics.

Integration into CAD Software

The adoption of spline modeling in computer-aided design (CAD) software marked a significant milestone in its evolution. Early CAD systems, such as CATIA and Autodesk's AutoCAD, integrated spline modeling techniques to enhance their modeling capabilities. This integration allowed designers and engineers to create more complex and precise models, revolutionizing the design process.

Companies like Autodesk and Dassault Systèmes played a crucial role in popularizing spline modeling through their innovative software solutions. These companies continually refined and expanded the capabilities of their CAD software, making spline modeling accessible to a broader audience and enabling its widespread use across various industries.

Impact and Legacy

Transformation of Design Processes

The introduction of spline modeling brought about a paradigm shift in design processes across multiple industries. In the automotive industry, spline modeling enabled the creation of aerodynamically efficient and aesthetically pleasing car designs. Aerospace engineers leveraged spline modeling to design complex aircraft components with high precision. The entertainment industry, particularly animation, saw a significant transformation as spline modeling allowed for the creation of lifelike characters and intricate visual effects.

Some of the most iconic designs and products owe their existence to the capabilities of spline modeling. The ability to create smooth, continuous curves and surfaces has empowered designers and engineers to push the boundaries of creativity and innovation.

Future Directions and Innovations

The future of spline modeling is poised for further innovation and enhancement, driven by emerging technologies such as machine learning and artificial intelligence. These technologies have the potential to automate and optimize various aspects of spline modeling, making it more efficient and accessible. The integration of AI algorithms can help in refining control points, optimizing shapes, and even generating new designs based on learned patterns.

The continuous evolution of spline modeling techniques promises to further revolutionize design software, enabling the creation of even more complex and intricate designs with greater efficiency and precision. The future holds exciting possibilities for the application of spline modeling in fields such as virtual reality, augmented reality, and advanced manufacturing processes.

Conclusion

Summary of Key Points

• Spline modeling is a mathematical technique used to create smooth and flexible curves and surfaces in computer graphics.
• The development of spline modeling was significantly influenced by the pioneering work of Pierre Bézier and Paul de Casteljau.
• Advancements in spline technology, such as the development of NURBS, have enhanced its capabilities and applications.
• Spline modeling has been integrated into CAD software, revolutionizing design processes in various industries.
• Emerging technologies like machine learning and artificial intelligence hold great potential for further enhancing spline modeling techniques.

Implications for Future Design Software

The continuous innovation in spline modeling is set to shape the future of design and engineering. As technologies evolve, spline modeling will become even more integral to the creation of complex and precise designs. The ongoing advancements will enable designers and engineers to explore new frontiers of creativity and innovation, ultimately leading to the development of cutting-edge products and solutions.